Expérience

    Pour cette expérience nous avons compter le taux d'hématie dans le sang d'un mouton (égal à celui de l'homme) pour savoir quel taux d'hématocrite un être normalement constitué doit avoir afin de comparer avec le taux d'hématie d'un humain ayant recours à de l'EPO.

    Pour cela, nous avons effectué un comptage au microscope à partir d'une cellule de Malassez, où nous avons déposé une goutte de sang à l'aide d'une pipette et du sang de mouton.

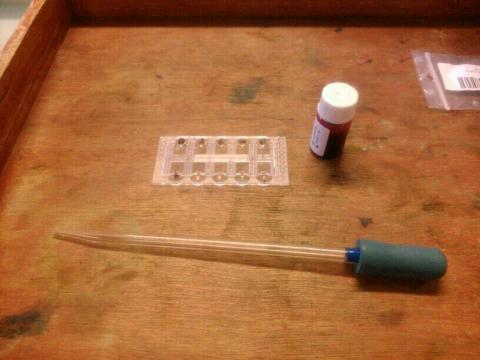
Une cellule de Malassez, une pipette et un tube de sang.

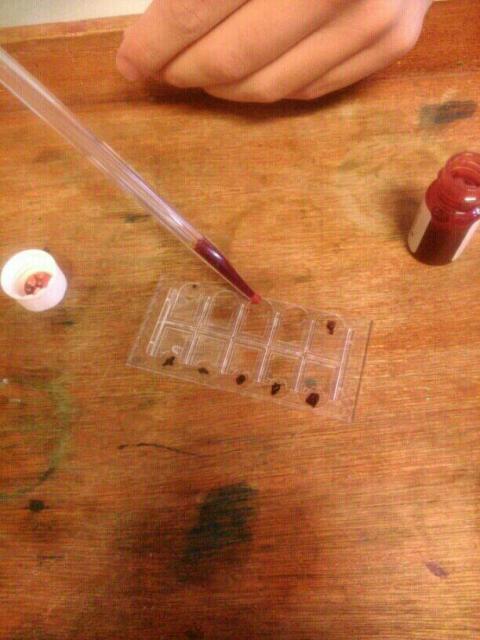
Dépôt d'une goutte de sang sur la cellule de Malassez

    Ensuite nous nous sommes rendus compte que le sang était trop épais, ainsi nous est venu l'idée de diluer avec du sérum physiologique dans le but de rendre le sang moins épais.

    Nous avons tout d'abord fait une dilution à un dixième, soit un dixième de millilitre de sang, puis une dilution à un centième car le premier était lui aussi trop épais.

Un tube de sérum physiologique.

Une dilution à un dixième (en bas) et une dilution à un centième (en haut).

Puis, nous avons donc observer la dilution à un centième au microscope :

Observation d'une dilution à un centième.

Cependant, la dilution à un centième n'était pas suffisante car le sang était encore trop épais. Nous avons par conséquent effectué une dilution à un millième (voir ci-dessous). La photo de droite ci-dessus à été effectué à l'aide d'une caméra que nous avons posé sur l'objectif du microscope.

Dilution du sang à un millième dans une fiole jaugée de 100mL.

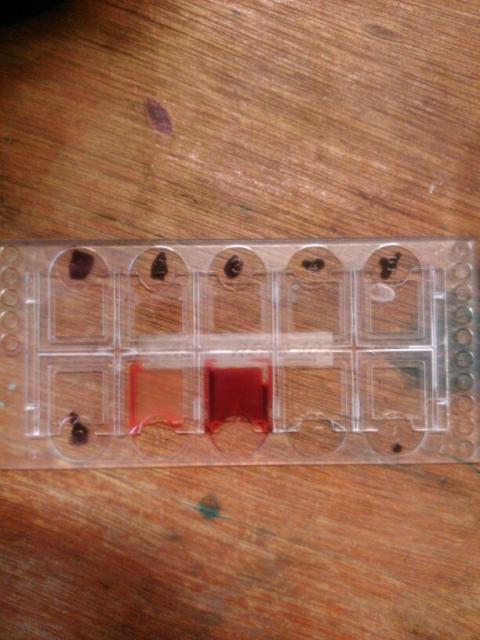
Second dépôt de sang dilué à un millième.

Voici alors le résultat que l'on a obtenu : 

La cellule de Malassez avec le résultat de la dilution à un millième.

    Nous avons capturé cette image à la suite d'une photo prise par la caméra du microscope, que nous avons déplacé sur un logiciel nous permettant de compter chaque hématie.

    Nous trouvons environ 100 000 globules rouges (100 x 1000 à cause de la dilution à un millième) dans une cellule de 0.00033 m de longueur, 0.00033 m de largeur et 0.00025 m de profondeur. Ainsi, le résultat est d'à peu près 3.67 x10¹⁵ (100000 / (0.00033 x0.00033 x 0.00025)) globules rouges par m³de sang. Ce qui équivaut à 3.67 millions de globules rouges par mm³ de sang (1 m³ =  1 000 000 000mm³ donc 3.67x10¹⁵ / 1x10⁹ = 3.67x10⁶). Ce qui est tout à fait dans les normes étant donné qu'une personne sainte est constituée d'un nombre total de globules rouges compris entre 3.5 millions et 6 millions de globules rouges par mm3 de sang.

    Nous pouvons donc en conclure que si les contrôles anti-dopages utilisent la même méthode que celle-ci, c'est alors un résultat semblable à celui ci-dessus qu'ils devraient trouver.